Mojo Lama

Last time around we got our feet wet — or was it ‘our hands dirty’? — with SuperColliderAU, working our way through some example code and building a simple Audio Unit plug-in from scratch (see Part 1 and Part 2 of Building Audio Units Using SuperColliderAU if you’re coming here for the first time).

This time we’re going to attempt something just a little bit more ambitious: designing, prototyping and building a full blown tremolo audio effect plug-in.

Why tremolo? Well, for one thing tremolo is a popular effect with a long and storied history in the annals of — how shall we say? — electrically-engendered popular music (did you know that Bo Diddley built his first tremolo unit using some auto parts and a wind-up clock?).

For another, the signal processing concepts behind the effect are fairly easy to come to grips with. To wit: tremolo is the use of a low frequency cyclical audio signal for varying the amplitude (loudness) of another audio signal.

In plain English: it’s like having someone twiddle the volume control on your guitar amp, TV, iPod, hearing aid, vibrator — whatever — up and down, up and down in a regular sort of repeating motion (did we mention that tremolo is sexy?).

It doesn’t get much simpler than this.

Here’s The Plan

We won’t be taking the straight ‘do this then do that’ tutorial approach here: our focus will be on process and tools as much as on actual building, and we’ll begin quite simply by imagining how to go about creating a tremolo effect. Then we’ll construct a suitable algorithm — a tremolo recipe, so to speak — through trial and error, testing our ideas along the way using SuperCollider’s graph-plotting capabilities.

Finally, in the next installment, we’ll set up a testing environment in SuperCollider so we can run the effect on the synth server, hear what it sounds like and refine our feature set. When we’re happy with what we’ve got, we’ll convert the effect to an Audio Unit plug-in, install it to our system, validate it and give it a test run in a couple of host applications.

What You’ll Need

Obviously, you’ll need to have SuperCollider installed on your Mac and a copy of the SuperColliderAU component in your default plug-in folder. You’ll also need to install and activate the AudioUnitBuilder quark extension (and suitably modify it if you running Lion or Mountain Lion) from within SuperCollider. All are described in the two posts referred to above.

What To Expect

Note this will not be is a tutorial on how to use Supercollider (see the SuperCollider Help files for that) though yeah, sure, you may pick up a technique or two along the way.

Also note that the algorithm used here isn’t necessarily the only, or the definitive, or even the simplest way to produce a tremolo effect (see Apple’s Audio Unit Programming Guide for at least one other method of crunching the numbers). It just happens to be my way.

And with those caveats out of the way, let’s get things rolling and begin where all good audio effect design begins: in our heads.

A Basic Tremolo Unit

We’ll start by thought-prototyping a simple monophonic tremolo effect. We’ve agreed that this involves using one signal (the modulating signal) to vary the loudness of another (the input signal).

Now, let’s stop right there: what exactly do we mean by a “modulating signal”?

Well, the modulating signal is going to consist of a simple up and down waveform, cycling repeatedly between silence and some maximum level — this will be the “hand” that twiddles the “volume control”.

And the effect we want it to have on the input signal is very straightforward indeed: when the modulator is silent, the input signal is silent (as if someone has turned the volume all the way down) and when the modulator is at its maximum, the input is at its maximum (as if the volume has been turned all the way back up). So there’s a direct correlation between this cycling of the modulating signal and the volume of the input signal.

But what are we modulating here? The loudness of another audio signal, obviously, but what are we really modulating? Ah, right — this is digital signal processing, so of course: we’re modulating numbers.

Let us, then, rephrase the effect we’re looking for: when the modulating signal is silent (its level is 0) the input signal is also silent (because the numbers that make up the input signal are being multiplied by 0); when the modulating signal is at it’s peak (its level is 1) the input signal is at its original level (because the input numbers are being multiplied by 1); and when the modulating signal is at any point in between (like 0.5) the input signal is scaled (multiplied) by the same amount.

So that’s our starting point: input signal x modulating signal = processed signal.

Setting Up Our Plotting Tools

It would be nice if we could give this bit of theory a dry run before building anything, so let’s use SuperCollider’s graph-plotting capabilities to piece things together one element at a time and see where it gets us.

Open a new document in SuperCollider and type in the following skeleton code:

(
	a = { 

	}.plot(2.0);

	a.minval = -1.0;
	a.maxval = 1.0;
)

All we’re doing here is:

• setting up an empty function definition (the curly brackets and everything between them; we’ll begin filling this in momentarily);
• calling SuperCollider’s Plot method on that function (Plot will create a graph of whatever we put into the function. The “2.0” in parentheses says we want the graph to plot over 2.0 seconds); and
• assigning the whole thing to a global variable called “a” so the function can be referred subsequent to its definition (as we’re doing here with the a.minval and a.maxval lines).

The outer parentheses are merely for selecting and executing the code; the minval and maxval methods set the minimum and maximum values for the graph (I’ll omit these going forward to save space).

Graphing It Out

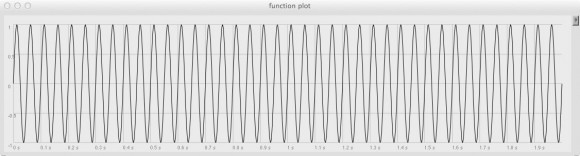
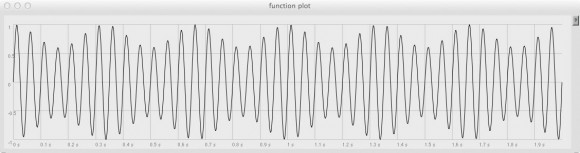
Now, let’s imagine our input is a nice, steady 20Hz sine wave test tone (in reality, 20Hz is far too low in pitch to be of much use as an audio source, but for graphing purposes it will do nicely).

Add the following to our code block:

(
	var input;

	a = { 
		input = SinOsc.ar(20, 0, 1.0); 
		input;	
	}.plot(2.0);
)

Here we’ve added a local variable called input to hold our input signal. Then, in the body of the function, we’re assigning to input a Sine Oscillator UGen running at 20Hz with 0 phase deviation and an amplitude of 1.0 (that’s full gain: maximum undistorted level).

The last thing we do in the function is simply call input — i.e., our sine generator — which therefore becomes the function’s return value (which, in turn, is what Plot is going to graph for us).

Double click just to the right of the opening parenthesis, so the entire block becomes selected, and hit ENTER (not RETURN). This will produce a new window containing a graph of our 20Hz “input” signal (you may need to resize the Plotter window to get it to look exactly like mine):

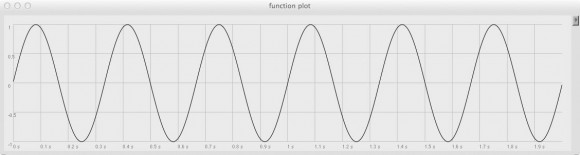
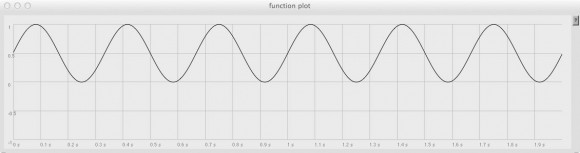
Next, we need a modulating signal (we’ll call it tremWave). For a tremolo effect, we’ll want this signal to run at a sub-audio frequency (for classic tremolo effects, that’s usually somewhere around 1 – 6Hz). We’ll go with a 3Hz sine wave here, again set at maximum gain.

Revise the code block as follows:

(
	var input, tremWave;

	a = { 
		tremWave = SinOsc.ar(3, 0, 1.0);
		input = SinOsc.ar(20, 0, 1.0); 
		tremWave;	
	}.plot(2.0);
)

Select the code block as before and hit ENTER to run the Plotter. Here’s what 2 seconds of our modulating waveform looks like:

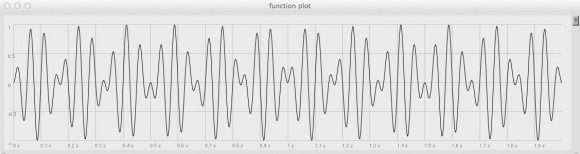
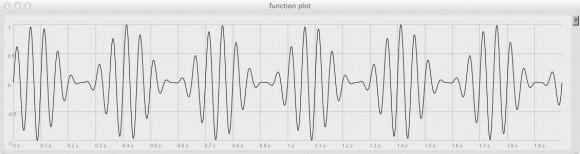
Now let’s see what we get when we multiply these two signals with each other…

(
	var input, tremWave;

	a = { 
		tremWave = SinOsc.ar(3, 0, 1.0);
		input = SinOsc.ar(20, 0, 1.0); 
		input * tremWave;	
	}.plot(2.0);
)

…and run the Plotter again:

Refining The Algorithm

Right off the bat there are a couple of problems. For one thing, the processed signal has twice as many peaks as the modulating signal (12 where we would have expected 6). For another, the ‘dips’ never quite settle in around 0 (i.e., silence) as they should. What’s going on here?

We goofed.

Our assumption was that the modulating signal would vary the input signal’s gain between silence (0) and full gain (1). But tremWave, of course, travels between -1 and 1: that is, between 0 and 1 in the first half of its cycle, and between 0 and -1 in the second half.

In other words, each full cycle of the modulating wave has two peaks: one positive and one negative. (We’ve inadvertently stepped into Amplitude Modulation territory, but that’s another post and not quite the interaction we had in mind here.)

What we need to do is somehow offset the modulating waveform so that it travels between 0 (silence) and 1 (full volume) rather than between -1 and 1.

Creating an Offset for the Modulating Signal

Looking at tremWave, we might imagine that if we were to add something to the signal — remember, the waveform is quite literally a moving number — we could lift the entire waveform so that the lowest point in its cycle — currently -1 — would be shifted up to 0.

How much do we need to add to accomplish this? In this particular case it would be the difference between -1 and 0 (that is, 1) but the amount will vary with different gain settings for tremWave. So the more complete answer is: half the height of the waveform.

You can think of it like this: currently, half the waveform is ‘above ground’ (‘ground’ here being 0, or silence) and half is ‘below ground’. What we need to do is make an adjustment so that the ‘below ground’ half sits ‘on the ground’. That means raising the entire waveform by half its height; this will always give us a signal whose lowest excursion point — regardless of its gain level — reaches down to zero, but never below zero.

The wrinkle, of course, is that making such an adjustment is going to raise the peaks by an equivalent amount — in this case, up to a level of 2.0 — which we most certainly do not want to do! The solution here is to enforce a maximum gain setting of 0.5 for the modulating signal.

Let’s do that now by changing tremWave‘s gain factor to 0.5 and running the Plotter on it:

(
	var input, tremWave;

	a = { 
		tremWave = SinOsc.ar(3, 0, 0.5);
		input = SinOsc.ar(20, 0, 1.0); 
	        tremWave;	
	}.plot(2.0);
)

Next, we’ll create a new variable to hold an offset copy of tremWave (we’ll call this new variable modulator).

Observe that although tremWave has had its gain scaled back to 0.5, it has a ‘full height’ of 1.0 — 0.5 ‘below ground’ and 0.5 ‘above’ — so we’re adding half of that (0.5) to it in order to get the proper offset:

(
	var input, tremWave, modulator;

	a = { 
		tremWave = SinOsc.ar(3, 0, 0.5);
		modulator = tremWave + 0.5;
		input = SinOsc.ar(20, 0, 1.0); 
                tremWave;
	}.plot(2.0);
)

Running the Plotter on modulator (i.e., tremWave plus offset)…

(
	var input, tremWave, modulator;

	a = { 
		tremWave = SinOsc.ar(3, 0, 0.5);
		modulator = tremWave + 0.5;
		input = SinOsc.ar(20, 0, 1.0); 
                modulator;
	}.plot(2.0);
)

…gives us:

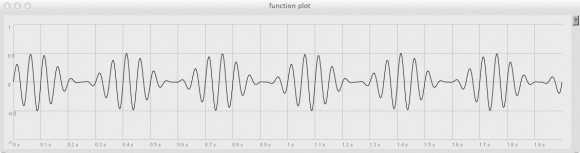
And if we now process our input with modulator, rather than directly with tremWave…

(
	var input, tremWave, modulator;

	a = { 
		tremWave = SinOsc.ar(3, 0, 0.5);
		modulator = tremWave + 0.5;
		input = SinOsc.ar(20, 0, 1.0); 
		input * modulator;	
	}.plot(2.0);
)

…the result looks like this:

That’s much better!

Adding a Depth Control

Now, we don’t necessarily want the signal’s gain to always travel from 0 (silence) to 1 (maximum output). We might, for example, wish to achieve a more subtle effect whereby the original signal never reaches silence, but simply exhibits an undulating “dip’ in its level.

To do this we need to be able to control the amount of modulation being applied to the input signal; that is, we need a depth control to scale the level of the modulating signal itself.

Let’s set that up now. First, we’ll add a new variable called depth and set it to 0.5 (the maximum gain setting we’ve determined we can allow for modulation between 0 and 1). Then we’ll use this new variable to replace both the gain setting for tremWave and the offset for modulator:

(
	var input, tremWave, modulator, depth=0.5;

	a = { 
		tremWave = SinOsc.ar(3, 0, depth);
		modulator = tremWave + depth;
		input = SinOsc.ar(20, 0, 1.0); 
		input * modulator;	
	}.plot(2.0);
)

Now let’s see what happens when we change the depth setting to, say, 0.25 (half it’s maximum level):

(
	var input, tremWave, modulator, depth=0.25;

	a = { 
		tremWave = SinOsc.ar(3, 0, depth);
		modulator = tremWave + depth;
		input = SinOsc.ar(20, 0, 1.0); 
		input * modulator;	
	}.plot(2.0);
)

Mmm… our signal just got tiny! Specifically, the overall level of the processed signal has dropped by half. Again, not quite what we intended.

What we really want to do here is have the modulation occur downward from the input signal’s original level — not up from silence.

How do we do that? Well, we know that a level of 1.0 on our modulating signal represents the original level of the input signal (because we’re multiplying the input signal by 1). We also know that depth represents the ‘height’ of tremWave.

So subtracting depth from 1 should get us a baseline level from which the modulating signal, at its peak, will always equal 1, and at its lowest point it will equal whatever depth is set to (0 — or silence — if depth is set to its maximum 0.5 level).

All we need to do is perform the subtraction to get our baseline, then add tremWave to it to get our modulation. Let’s give it a try:

(
	var input, tremWave, modulator, depth=0.25;

	a = { 
		tremWave = SinOsc.ar(3, 0, depth);
		modulator = (1.0 - depth) + tremWave;
		input = SinOsc.ar(20, 0, 1.0); 
		input * modulator;	
	}.plot(2.0);
)

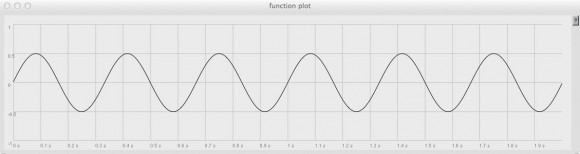
And again, with depth set to it’s maximum 0.5 level:

Ah! There’s our recipe for tremolo.

And just in the nick of time, too — the Word Count Fairy is giving me a very stern look, so gotta go. See you for Part 2?